VOMMA VANNA E VETA

Introduzione

Cosa sono le Greche.

Sappiamo che le greche sono valori che ci aiutano a mettere in relazione il prezzo di un’opzione con le sue determinanti fondamentali (prezzo strike, prezzo del sottostante, tempo a scadenza, volatilità, interesse, dividendi).

Abbiamo visto nei numerosi video su Sunnymoney le greche di primo ordine. Il Delta, che è la relazione del prezzo con il sottostante; il Theta, che è la relazione con il tempo; il Vega, con la volatilità; il Rho, con il tasso di interesse. Abbiamo inoltre più volte parlato del Gamma, che è una greca di secondo ordine, e della sua importanza nella gestione di un portafoglio in opzioni. È definita di secondo ordine in quanto mostra la variazione di una greca rispetto a una determinante fondamentale del prezzo di un’opzione. Il Gamma infatti mostra la variazione del Delta al variare del sottostante.

Oggi andiamo ad approfondire le greche di secondo ordine direttamente collegate alla volatilità: Vomma, Vanna e Veta.

Cosa sono Vomma, Vanna e Veta

Il Vomma misura la variazione del Vega, in base alle variazioni della volatilità implicita. In altre parole il Vomma è una misura seconda della volatilità.

Il Vanna invece misura la variazione del Delta in base alle variazioni della volatilità implicita.

Il Veta misura la variazione del Theta in base alla variazione della volatilità implicita.

Facciamo un esempio per cercare di comprendere meglio gli effetti della volatilità implicita sul Vega, sul Delta e sul Theta, e poi come questi influiscono direttamente sul valore di una opzione.

Prendiamo il nostro simulatore e apriamo una semplice posizione long Put.

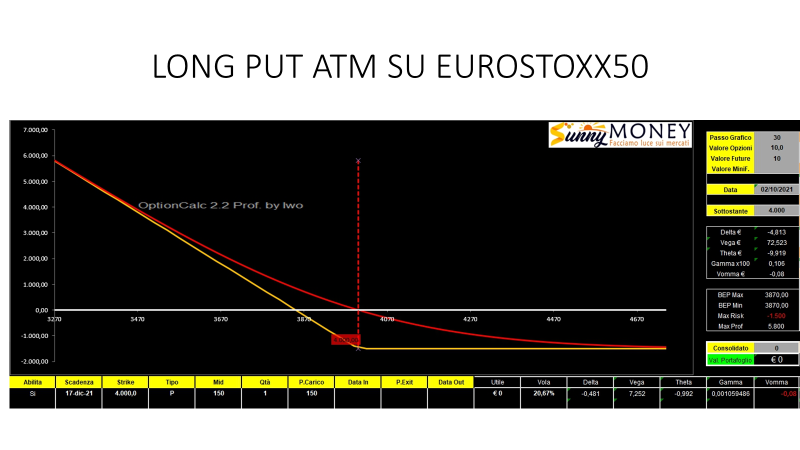
Supponiamo di avere in portafoglio una opzione Put Atm su Eurostoxx50 con scadenza 75 giorni con un moltiplicatore 10, ovvero ogni punto equivale a 10 Euro. La long put ha un valore di 150 punti, una volatilità del 20.67%, un Delta di -0,48, un Theta di -9 euro, ed un Vega di 72,5 euro. Questo vuol dire che ogni aumento dell’1% di volatilità implicita corrisponde ad un aumento di 72 euro o 7.2 punti di premio. Notiamo che il Vomma ha un valore prossimo allo ZERO e quindi è praticamente ininfluente.

Quindi, simuliamo un aumento di 10 punti percentuali di volatilità, da 20.67% a 30.67%, ed ecco cosa succede alla nostra put ATM.

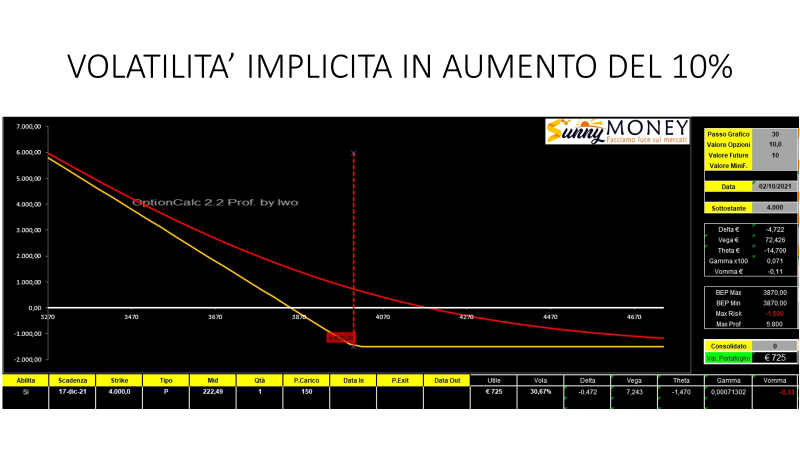
Con questa long put a seguito di un aumento di volatilità implicita abbiamo guadagnato 725 euro. Questa somma equivale esattamente a 10 volte il Vega prezzato, che vi ricordo era di 72,5 euro per ogni punto base.

Come è evidente dai numeri, il nostro Delta, il nostro Vega ed il Vomma sono rimasti sostanzialmente simili. A cambiare, oltre al premio dell’opzione, è ovviamente il Theta, che è aumentato e quasi raddoppiato. La variazione di Theta a seguito di un cambiamento della volatilità implicita si può misurare con il Veta. Il theta è passato dagli originari -9 euro agli attuali -14 euro.

Ebbene, il Vomma, come abbiamo visto in questo esempio, è molto basso sulle opzioni ATM. Mentre il proposito del prossimo esempio è mostrarvi che il Vomma ha un valore e un effetto importante sulle opzioni OTM, rendendole strumenti spesso esplosivi nelle mani di ignari venditori.

Facciamo infatti un altro esempio, e compriamo una long put OTM a strike 3500 con scadenza 75 giorni.

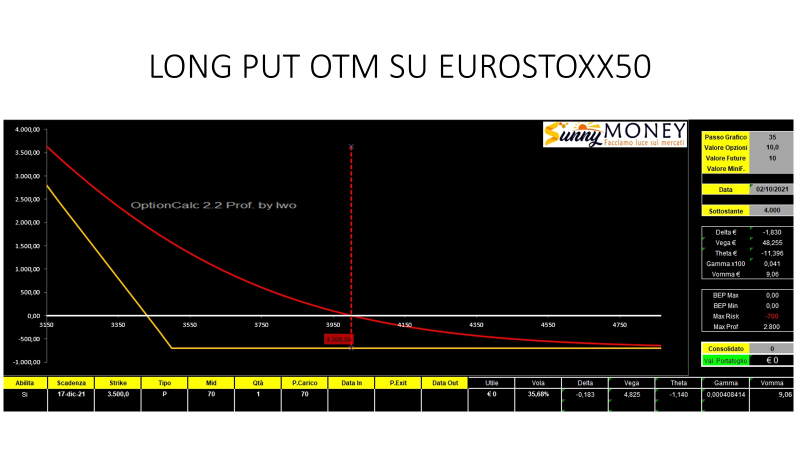
In questo caso, con un premio di 70 punti abbiamo un Delta di -0.18, un Vega di 48 euro, un Theta di -11 ed un Vomma di 9 euro a fronte di una volatilità implicita di 35.6%

Come nel caso precedente è facile comprendere che per ogni punto di aumento di volatilità implicita il prezzo dell’opzione dovrebbe aumentare di 48 euro circa, e quindi un aumento di 10 punti dovrebbe corrispondere ad un aumento del premio di 480 euro.

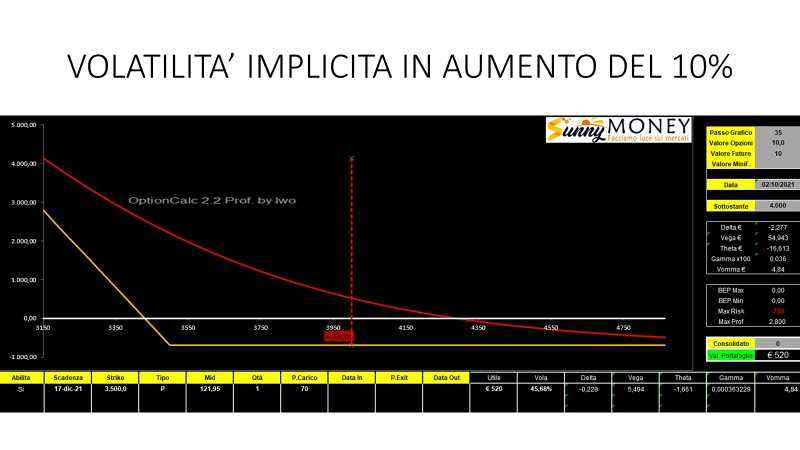
Andiamo a vedere se realmente è così, e come si sono modificate le greche. Simuliamo appunto un aumento di 10 punti percentuali e portiamo la volatilità implicita da 35.6% a 45.6%.

La prima cosa che balza all’occhio più attento è che in realtà l’aumento di Vega dovuto all’aumento di 10 punti di volatilità NON ha prodotto un aumento di premio in modo lineare di 480 euro. In realtà il premio è aumentato di 520 euro, ben 40 euro in più di quanto ipotizzato precedentemente, quasi il 10%.

Perché?

Il motivo principale è che nelle opzioni OTM la volatilità implicita impatta sul Vega in modo più che proporzionale. Questa misura è il Vomma. Infatti con volatilità implicita al 35,6% avevamo un Vomma di 9 euro. Bene, quel Vomma, all’aumentare della volatilità implicita, si è trasferito direttamente nel Vega, appunto rendendo il calcolo della posizione non più lineare come succede normalmente per le opzioni ATM, ma esponenziale, ovvero il prezzo aumenta in modo più che proporzionale. E considerata la reattività delle opzioni OTM, ecco perché il prezzo letteralmente esplode quando siamo in fast market.

Questo aumento di 10 punti di volatilità implicita ha portato di fatto il Vega al valore di 55 euro ed il Vomma a ridursi, passando da 9 a 4.8 euro.

Se notate, anche il Delta passa da -0.18 a -0.22. Questa variazione di Delta è misurata dal Vanna. E anche il Theta ha subito un effettivo balzo in avanti, passando da 11 a 16 euro di decadimento temporale. Questa variazione è misurata dal Veta.

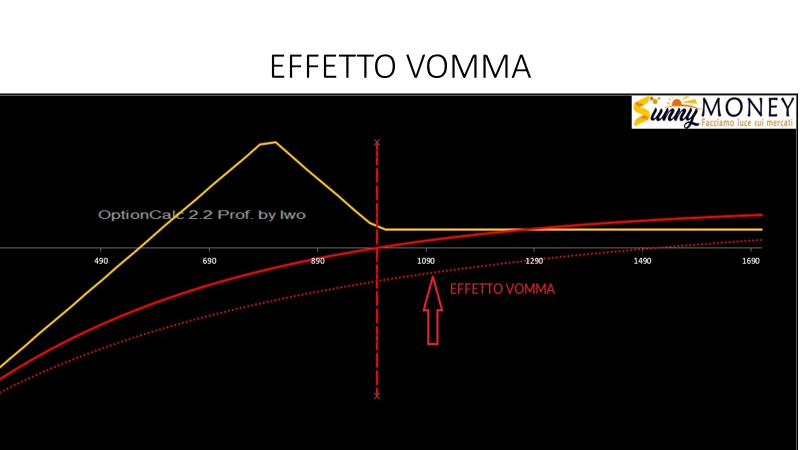
Quindi se il Vega ha una relazione lineare tra il premio e la volatilità di una opzione, il Vomma invece esprime la sua convessità. Questo vuol dire che utilizzando solo il Vega e non considerando il Vomma si notano, a fronte di aumenti di volatilità implicita, variazioni e divari sempre maggiori tra il prezzo che abbiamo stimato ed il prezzo effettivo. Il Vomma è appunto la misura di questa differenza, fra valore teorico dato da un determinato valore di Vega ed un valore reale dell’opzione dato dal cambiamento più che proporzionale del Vega stesso.

Utilizzando solo il Vega è facile sottostimare il reale valore di una opzione dovuto ad aumento di volatilità. Invece, inserendo nel nostro calcolo anche il Vomma, riusciremo ad avere una misura di premio il più realistica possibile.

Al contrario se la volatilità implicita scende, il valore del Vega tenderà a sovrastimare il premio delle opzioni. Anche in questo caso applicare il Vomma al Vega permette di riuscire a determinare con maggior precisione il reale valore del premio di una determinata opzione.

Su queste importanti proprietà del Vega ho costruito un mio modello operativo, assolutamente replicabile e adatto, con i dovuti accorgimenti, a tutti i mercati finanziari e che ho spiegato con dovizia di particolari in un corso che ho chiamato “Vendere Vega comprando Delta: obiettivo 20%”

Di fatto, per chi conosce e segue l’operatività su Sunnymoney, cerchiamo di prendere vantaggio dagli eccessi di volatilità che spesso si verificano sui mercati al raggiungimento di determinati livelli di probabilità.

Trovate il corso a questo link: https://www.sunnymoney.it/videocorsi-a-pagamento/vendere-vega-menu/